Parameter Sharing in Deep Learning

In a previous post I have talked about multitask learning (MTL) and demonstrated the power of MTL compared to Single-Task Learning (STL) approaches. In this post, I will stay under the general topic of MTL, and present a different approach for MTL using parameter sharing in neural networks. Also, I will provide the relevant code for the main models (in PyTorch). Lastly, I will show an interesting use of MTL, to achieve high accuracy in tasks for which data is scarce.

MTL for Deep Learning

The two dominant approaches for performing MTL with neural networks are hard and soft parameter sharing, in which we seek to learn shared or “similar” hidden representation(s) for the different tasks. In order to impose these similarities between tasks, the model is simultaneously learned for all tasks and with some constraint or regularization on the relationship between related parameters.

There are some more complex methods for MTL with neural networks (see e.g. [1], [2]), which I won’t cover here. More examples can be found in [3], [4].

Hard Parameter Sharing

Perhaps the most widely used approach for MTL with NNs is hard parameter sharing ([5]), in which we learn a common space representation for all tasks (i.e. completely share weights/parameters between tasks). This shared feature space is used to model the different tasks, usually with additional, task-specific layers (that are learned independently for each task). Hard parameter sharing acts as regularization and reduces the risk of overfitting, as the model learns a representation that will (hopefully) generalize well for all tasks.

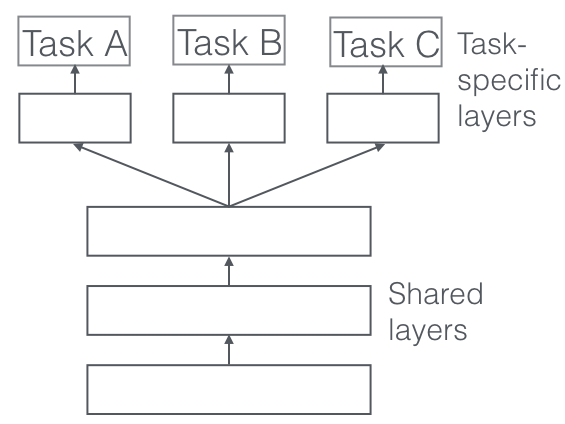
Example of hard parameter sharing architecture. Source: An Overview of Multi-Task Learning in Deep Neural Networks.

Recently, Andrej Karpathy from Tesla gave a talk about how multitask learning (with hard parameter sharing) is used for building Tesla’s Autopilot. He also reviewed some of the fundamental challenges and open questions in MTL. In natural language processing (NLP), MTL was utilized to train a single model without any task-specific modules or parameters, for solving ten NLP tasks ([6]).

A simple implementation of hard parameter sharing with feed-forward NN is given below. You can control the number of layers to share, and the number of task-specific layers.

Click on code to expand/collapse

Soft Parameter Sharing

Instead of sharing exactly the same value of the parameters, in soft parameter sharing, we add a constraint to encourage similarities among related parameters. More specifically, we learn a model for each task and penalize the distance between the different models’ parameters. Unlike hard sharing, this approach gives more flexibility for the tasks by only loosely coupling the shared space representations.

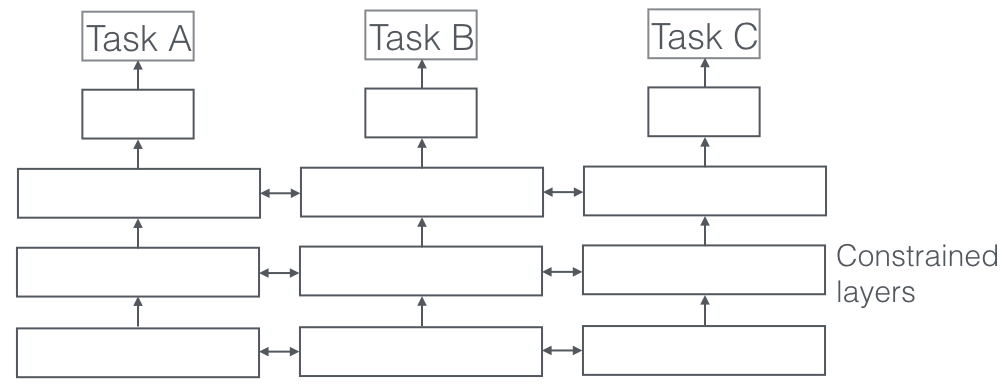
Example of soft parameter sharing architecture. Source: An Overview of Multi-Task Learning in Deep Neural Networks.

Assume we are interested in learning 2 tasks, \(A\) and \(B\), and denote the \(i\)th layer parameters for task \(j\) by \(W_i^{(j)}\). One possible approach to impose similarities between corresponding parameters is to augment our loss function with an additional loss term,

\[\mathcal{L}=\ell + \sum_{S(L)} \lambda_i \Vert W_i^{(A)}-W_i^{(B)}\Vert_F^{2}\]

where \(\ell\) is the original loss function for both tasks (e.g. sum of losses), and \(\Vert\cdot\Vert_F^{2}\) is the squared Frobenius norm. [7] proposed a similar approach for cross-lingual parameter sharing in NLP.

Another approach is to penalize the nuclear or trace norm of the tensor obtained by stacking together \(W_i^{A}\) and \(W_i^{B}\). The traced norm is defined as the sum of singular values \(\Vert W \Vert = \sum_i \sigma_i\). This penalty was originally proposed in the context of linear models (see e.g. [8]), to replace rank constraints in Reduced Rank Regression. This type of penalty encourages sparsity in the factor space and at the same time gives shrinkage coefficient estimates and thus conducts dimension reduction and estimation simultaneously.

An implementation of soft parameter sharing with \(L_2\) regularization is given below.

Click on code to expand/collapse

MTL for Handling Scarce Data

As promised, I will show how MTL can be used in cases where data is scarce for some of the tasks, but available for others. Consider a time series of the daily taxi rides in NYC for two vendors. Assume we have about one year and ten months of training data for vendor \(A\), but only ~3 months of data for vendor \(B\). In this case, it is impossible to model the yearly seasonality by using an STL approach for modeling task \(B\). Instead, we will use MTL with hard sharing to model both tasks, hence making it possible to learn yearly and holiday effects for task \(B\) using ~3 months of data only (!). We mask the loss associated with missing observations (from task \(B\)), to explicitly exclude unobserved values from all calculations and weights updates. The results of forecasting 90 days into the “future” are shown in the figure below (and are mind-blowing 🤯),

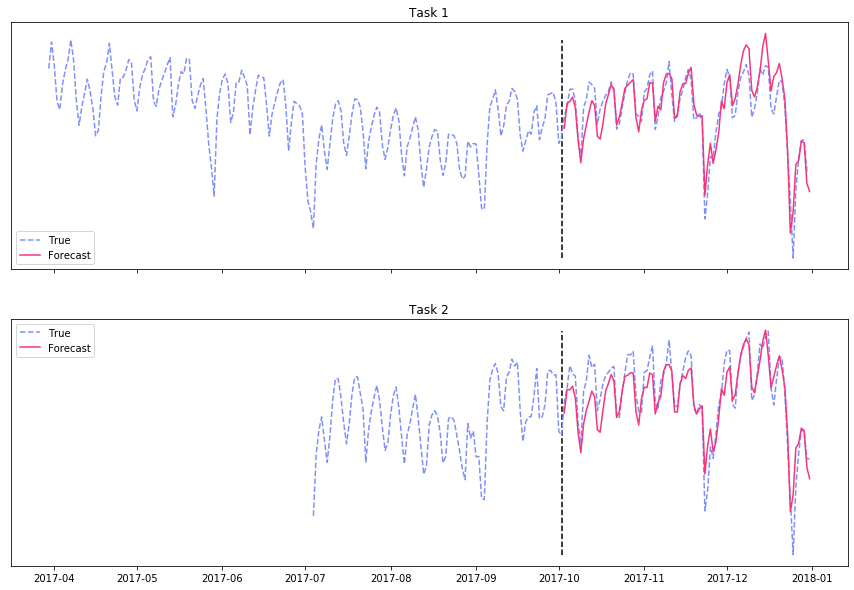
Overcoming scarce data using multitask learning.

To emphasize how awesome this is, here’s the result of fitting Facebook’s Prophet, a single task learning method, to the 3 months of training data for task \(B\):

Multitask learning vs. Prophet (STL).

Nice!

Conclusion

In this post, I have introduced two methods of MTL for deep learning, hard and soft parameter sharing. In addition, I have shown how MTL can be utilized to boost performance in cases where data is scarce for some of the tasks.

I hope you have found this post useful. For any questions, comments or corrections, please leave a comment below.

---

References

[1] Long, M., & Wang, J. (2015). Learning Multiple Tasks with Deep Relationship Networks. arXiv Preprint arXiv:1506.02117.
[2] Misra, I., Shrivastava, A., Gupta, A., & Hebert, M. (2016). Cross-stitch Networks for Multi-task Learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition.
[3] Zhang, Yu, and Qiang Yang. A survey on multi-task learning. arXiv preprint arXiv:1707.08114 (2017).
[4] Ruder, S., 2017. An overview of multi-task learning in deep neural networks. arXiv preprint arXiv:1706.05098.
[5] Caruana, R. Multitask learning: A knowledge-based source of inductive bias. Proceedings of the Tenth International Conference on Machine Learning. 1993
[6] McCann, B., Keskar, N.S., Xiong, C. and Socher, R., 2018. The natural language decathlon: Multitask learning as question answering. arXiv preprint arXiv:1806.08730.
[7] Duong, L., Cohn, T., Bird, S. and Cook, P., 2015, July. Low resource dependency parsing: Cross-lingual parameter sharing in a neural network parser. In Proceedings of the 53rd Annual Meeting of the Association for Computational Linguistics and the 7th International Joint Conference on Natural Language Processing (Volume 2: Short Papers) (pp. 845-850).
[8] Yuan, Ming, Ali Ekici, Zhaosong Lu, and Renato Monteiro (2007). Dimension reduction and coefficient estimation in multivariate linear regression. In: Journal of the Royal Statistical Society: Series B (Statistical Methodology) 69.3, pp. 329–346.