In a previous post I have talked about multitask learning (MTL) and demonstrated the power of MTL compared to Single-Task Learning (STL) approaches. In this post, I will stay under the general topic of MTL, and present a different approach for MTL using parameter sharing in neural networks. Also, I will provide the relevant code for the main models (in PyTorch). Lastly, I will show an interesting use of MTL, to achieve high accuracy in tasks for which data is scarce.

MTL for Deep Learning

The two dominant approaches for performing MTL with neural networks are hard and soft parameter sharing, in which we seek to learn shared or “similar” hidden representation(s) for the different tasks. In order to impose these similarities between tasks, the model is simultaneously learned for all tasks and with some constraint or regularization on the relationship between related parameters.

There are some more complex methods for MTL with neural networks (see e.g. [1], [2]), which I won’t cover here. More examples can be found in [3], [4].

Hard Parameter Sharing

Perhaps the most widely used approach for MTL with NNs is hard parameter sharing ([5]), in which we learn a common space representation for all tasks (i.e. completely share weights/parameters between tasks). This shared feature space is used to model the different tasks, usually with additional, task-specific layers (that are learned independently for each task). Hard parameter sharing acts as regularization and reduces the risk of overfitting, as the model learns a representation that will (hopefully) generalize well for all tasks.

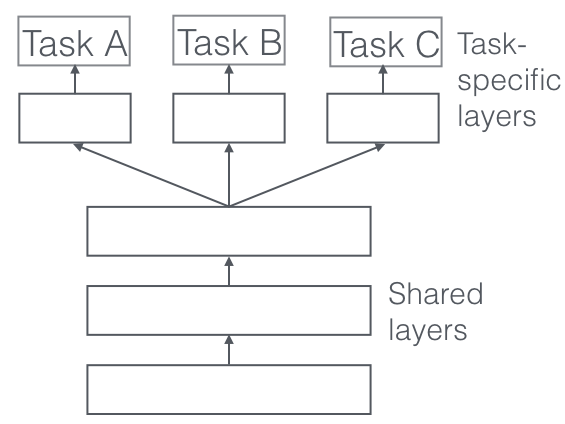
Example of hard parameter sharing architecture. Source: An Overview of Multi-Task Learning in Deep Neural Networks.

Recently, Andrej Karpathy from Tesla gave a talk about how multitask learning (with hard parameter sharing) is used for building Tesla’s Autopilot. He also reviewed some of the fundamental challenges and open questions in MTL. In natural language processing (NLP), MTL was utilized to train a single model without any task-specific modules or parameters, for solving ten NLP tasks ([6]).

A simple implementation of hard parameter sharing with feed-forward NN is given below. You can control the number of layers to share, and the number of task-specific layers.

Click on code to expand/collapse

Soft Parameter Sharing

Instead of sharing exactly the same value of the parameters, in soft parameter sharing, we add a constraint to encourage similarities among related parameters. More specifically, we learn a model for each task and penalize the distance between the different models’ parameters. Unlike hard sharing, this approach gives more flexibility for the tasks by only loosely coupling the shared space representations.

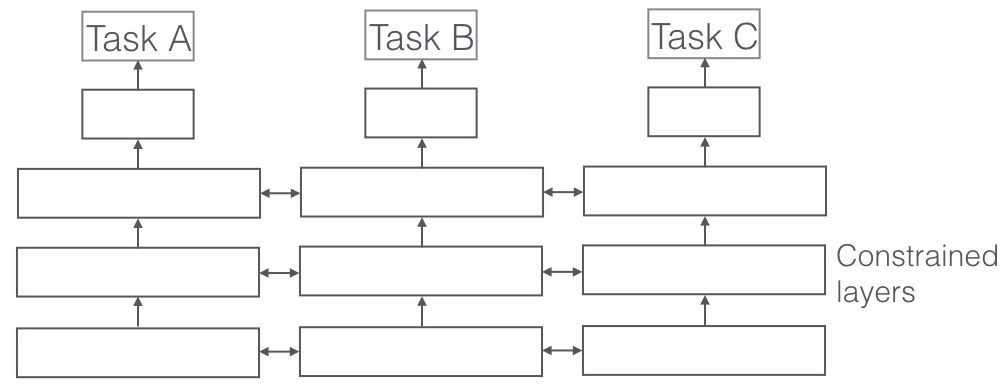
Example of soft parameter sharing architecture. Source: An Overview of Multi-Task Learning in Deep Neural Networks.

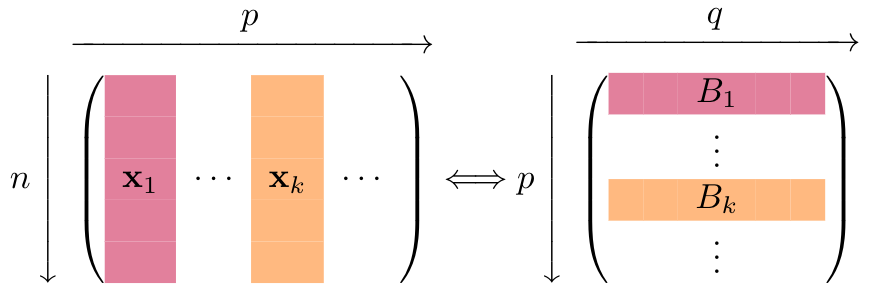
Assume we are interested in learning 2 tasks, \(A\) and \(B\), and denote the \(i\)th layer parameters for task \(j\) by \(W_i^{(j)}\). One possible approach to impose similarities between corresponding parameters is to augment our loss function with an additional loss term,

where \(\ell\) is the original loss function for both tasks (e.g. sum of losses), and \(\Vert\cdot\Vert_F^{2}\) is the squared Frobenius norm. [7] proposed a similar approach for cross-lingual parameter sharing in NLP.

Another approach is to penalize the nuclear or trace norm of the tensor obtained by stacking together \(W_i^{A}\) and \(W_i^{B}\). The traced norm is defined as the sum of singular values \(\Vert W \Vert = \sum_i \sigma_i\). This penalty was originally proposed in the context of linear models (see e.g. [8]), to replace rank constraints in Reduced Rank Regression. This type of penalty encourages sparsity in the factor space and at the same time gives shrinkage coefficient estimates and thus conducts dimension reduction and estimation simultaneously.

An implementation of soft parameter sharing with \(L_2\) regularization is given below.

Click on code to expand/collapse

MTL for Handling Scarce Data

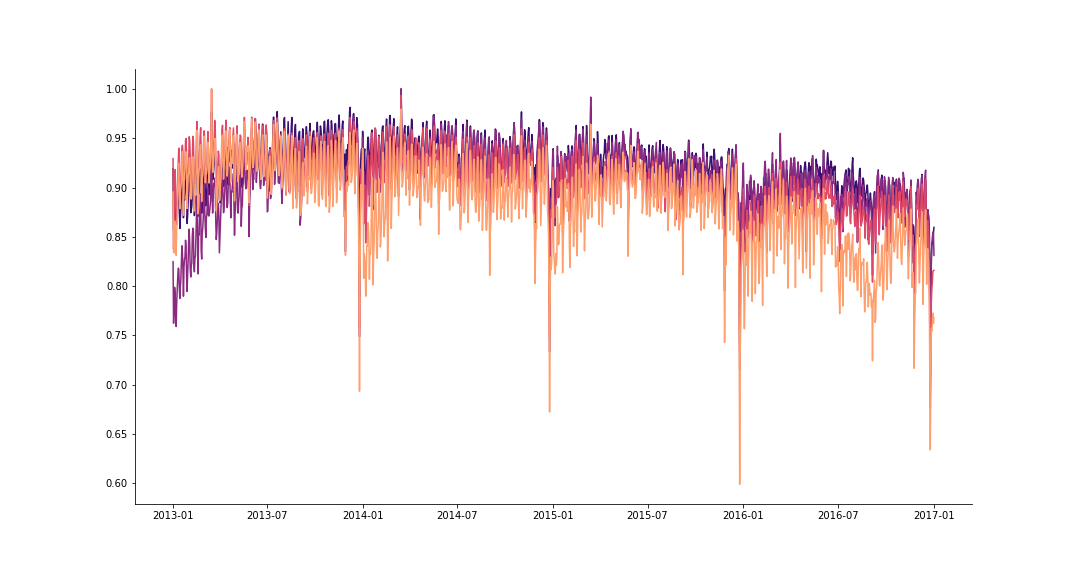
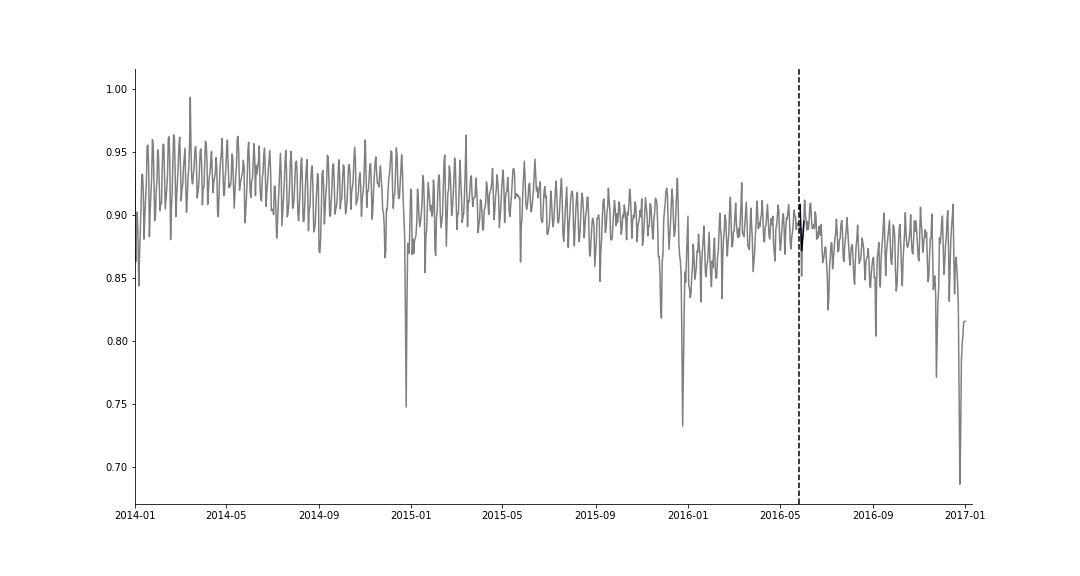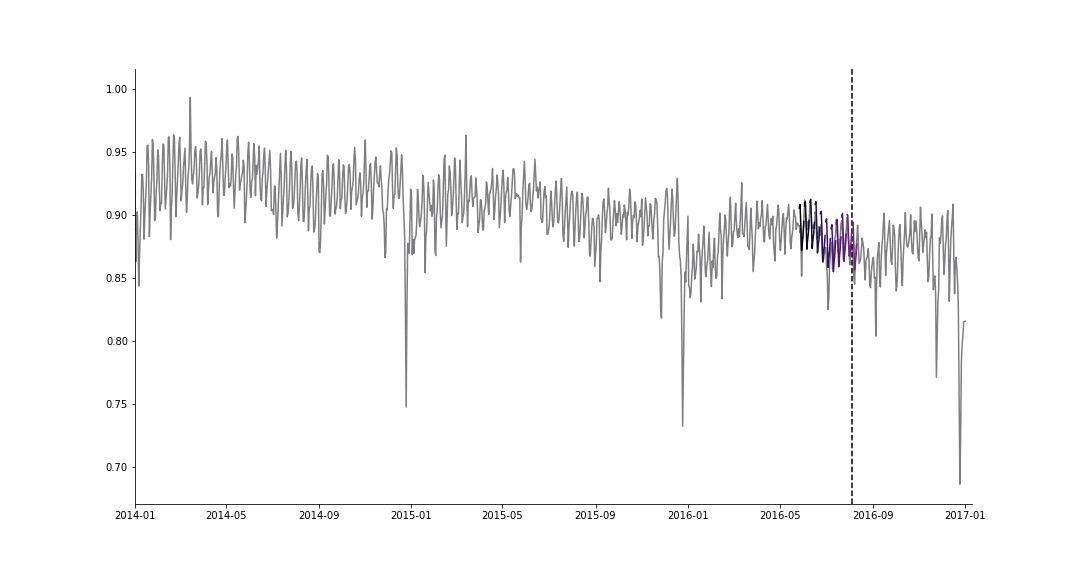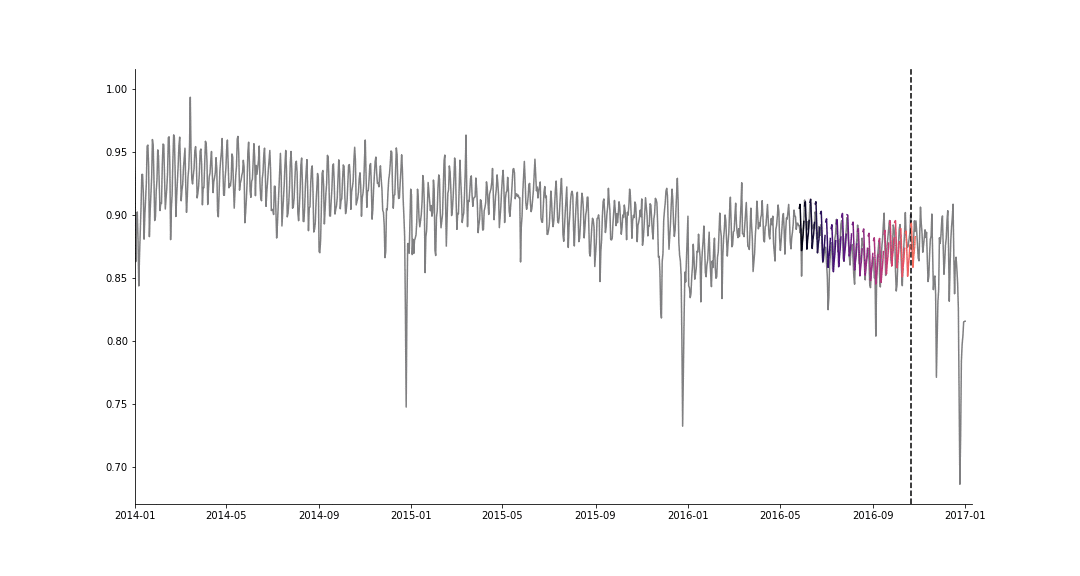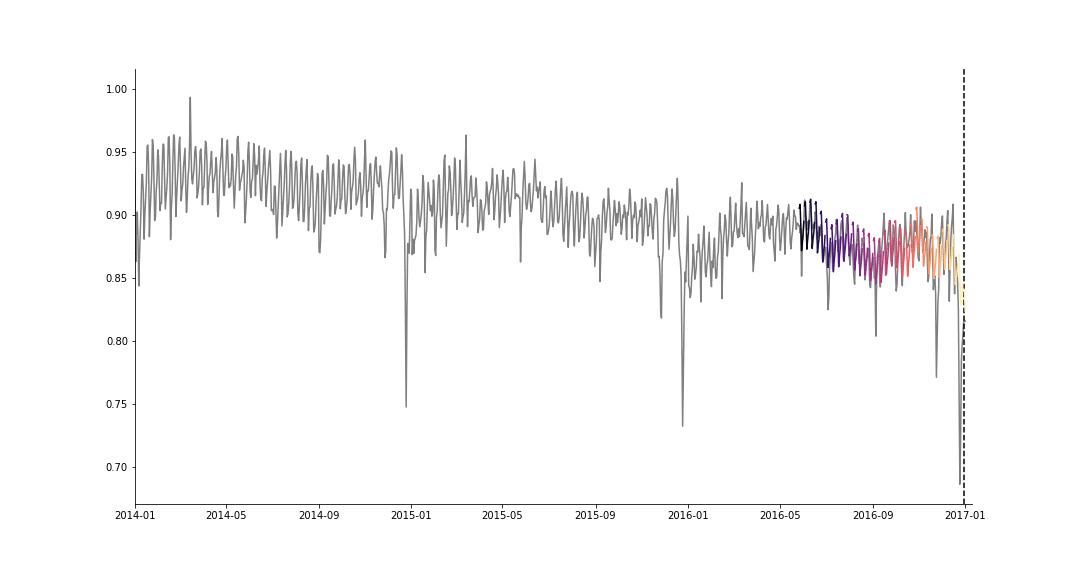
As promised, I will show how MTL can be used in cases where data is scarce for some of the tasks, but available for others. Consider a time series of the daily taxi rides in NYC for two vendors. Assume we have about one year and ten months of training data for vendor \(A\), but only ~3 months of data for vendor \(B\). In this case, it is impossible to model the yearly seasonality by using an STL approach for modeling task \(B\). Instead, we will use MTL with hard sharing to model both tasks, hence making it possible to learn yearly and holiday effects for task \(B\) using ~3 months of data only (!). We mask the loss associated with missing observations (from task \(B\)), to explicitly exclude unobserved values from all calculations and weights updates. The results of forecasting 90 days into the “future” are shown in the figure below (and are mind-blowing 🤯),

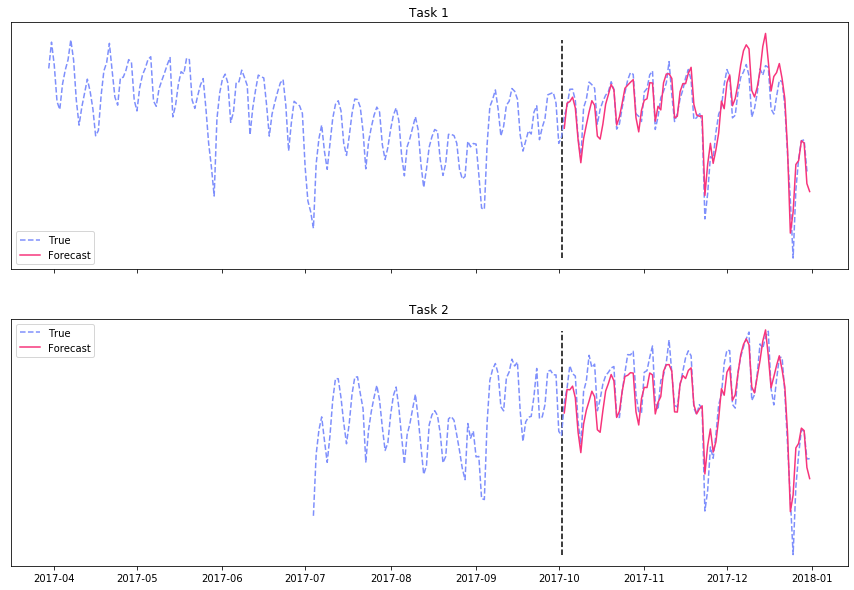
Overcoming scarce data using multitask learning.

To emphasize how awesome this is, here’s the result of fitting Facebook’s Prophet, a single task learning method, to the 3 months of training data for task \(B\):

Multitask learning vs. Prophet (STL).

Nice!

Conclusion

In this post, I have introduced two methods of MTL for deep learning, hard and soft parameter sharing. In addition, I have shown how MTL can be utilized to boost performance in cases where data is scarce for some of the tasks.

I hope you have found this post useful. For any questions, comments or corrections, please leave a comment below.

References

[1] Long, M., & Wang, J. (2015). Learning Multiple Tasks with Deep Relationship Networks. arXiv Preprint arXiv:1506.02117.
[2] Misra, I., Shrivastava, A., Gupta, A., & Hebert, M. (2016). Cross-stitch Networks for Multi-task Learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition.
[3] Zhang, Yu, and Qiang Yang. A survey on multi-task learning. arXiv preprint arXiv:1707.08114 (2017).
[4] Ruder, S., 2017. An overview of multi-task learning in deep neural networks. arXiv preprint arXiv:1706.05098.
[5] Caruana, R. Multitask learning: A knowledge-based source of inductive bias. Proceedings of the Tenth International Conference on Machine Learning. 1993
[6] McCann, B., Keskar, N.S., Xiong, C. and Socher, R., 2018. The natural language decathlon: Multitask learning as question answering. arXiv preprint arXiv:1806.08730.
[7] Duong, L., Cohn, T., Bird, S. and Cook, P., 2015, July. Low resource dependency parsing: Cross-lingual parameter sharing in a neural network parser. In Proceedings of the 53rd Annual Meeting of the Association for Computational Linguistics and the 7th International Joint Conference on Natural Language Processing (Volume 2: Short Papers) (pp. 845-850).
[8] Yuan, Ming, Ali Ekici, Zhaosong Lu, and Renato Monteiro (2007). Dimension reduction and coefficient estimation in multivariate linear regression. In: Journal of the Royal Statistical Society: Series B (Statistical Methodology) 69.3, pp. 329–346.

One of the fundamentals of the human learning process is that multiple tasks are learned in parallel, and not as independent tasks. Throughout this process, knowledge and experiences acquired in one task, are shared and transferred to the others. This general idea has been adopted in machine learning (ML) as well and has been shown to be beneficial in terms of learning efficiency and prediction accuracy. This subfield of ML is referred to as Multi-Task Learning (MTL).

In this post we will familiarize ourselves with the general concept of MTL and demonstrate the power of MTL compared to Single-Task Learning (STL) approaches, over the problem of multidimensional time-series forecasting.

Motivation

Multitask learning is an approach in which multiple learning tasks are solved simultaneously, in order to improve the generalization performance of the single tasks, by leveraging the information contained in the training signals of other tasks. In other words, MTL aims to improve the accuracy of task-specific models, by utilizing similarities and relations between the different problems.

In some cases, our main goal is indeed to optimize the model’s performance over a set of tasks, however, typically in ML, we are only interested in optimizing for a single task (e.g. STL regression/classification frameworks). Even if that is the case, it has been shown that adding additional learning problems (often referred to as auxiliary tasks), will allow us to improve upon our main (original) task. In the latter, MTL can be viewed as a regularization method, in which regularization is induced by optimizing the model’s performance over all tasks.

Background

Many approaches have been developed in order to learn multiple tasks simultaneously (see e.g. [1], [2]). Perhaps the most common approaches nowadays use (deep) neural networks (NN), in which information is transferred across tasks through hard/soft parameter sharing. The more “classical” ML approaches use linear models and kernel methods (and sometimes involves Bayesian approaches). In general, we can divide these approaches into two classes:

• Feature learning approaches, which involve either feature selection across tasks through norm regularization, or feature transformation (e.g. parameter sharing in NNs).
• Task relation learning approaches, in which task relations are used to enforce similarities between related tasks. These relations are assumed to be known a priori, or learned directly from the data.

To keep things simple, we are going to focus on a simple (and commonly used) linear approach, which induces cross-task feature selection (i.e. feature learning approache).

Problem Formulation

In the general case, each task might consist of its own training data, however, in many cases, the same set of explanatory variables, \(X\in\mathbb{R}^{n\times p}\), is used to model the different target variables, \(\textbf{y}_i \in \mathbb{R}^n\) for \(i=1,...,q\). For example, an on-demand transportation company may attempt forecasting demand and supply in different time frames and geographic locations. The general task of modeling multiple responses using a joint set of covariates can be expressed using multivariate regression (MR), or multiple response regression — a generalization of the classical regression model to regressing \(q > 1\) responses on \(p\) predictors. The multivariate regression model is given by,

where \(Y\in\mathbb{R}^{n\times q}\) denote the response matrix, \(B\) is a \(p \times q\) regression coefficient matrix, and \(E\) is an \(n \times q\) error matrix. A naive approach to the MR problem is to apply one of the STL methods, i.e. lasso, ridge, etc. to each of the \(q\) tasks independently. However, in many cases, the different problems are related, and this oversimplified approach fails to utilize all the information contained in the data.

Shared Information

The multivariate regression framework naturally induces a group structure over the coefficient matrix, in which every explanatory variable, \(\textbf{x}_{j}\) for \(j = 1, ..., p\), corresponds to a group of \(q\) coefficients, \(B_j\).

The multivariate regression framework naturally induces a group structure over the coefficient matrix.

One popular and simple approach for MTL that utilized this group structure, is the group lasso (see e.g. [3], [4]), in which a lasso-like penalty is placed over pre-defined groups of coefficients (this penalty is also referred to as \(L_1/L_2\)-penalty). The group lasso objective function is given by,

where \(\lambda\) is a regularization parameter \(\Vert \cdot \Vert_F\) is the Frobenius norm, and \(B_j\) is the \(j\)th row of \(B\). The \(L_1/L_2\)-penalty encourages coefficients within the same group to share a similar absolute value, and essentially perform cross-task variable selection, in which a variable (corresponds to a row in \(B\)) is either selected or omitted from all tasks. Thus, this method allows us to learn a common sparsity structure, and to recover the joint support — the set of variables that are relevant for all tasks.

Next, we compare the results of applying the MTL approach of group lasso to the STL lasso approach (applied for each task independently).

Forecasting Taxi Rides

We use the Chicago Taxicabs dataset which includes taxi trips from 2013 to mid. 2017, reported to the City of Chicago. We utilize the Fourier series to model the periodic effects of our multivariate time-series, similar to [5], [6]. For a seasonal period \(P\), this involves generating \(2\cdot N_p\) features of the form,

In addition, we incorporate covariates for the modeling of a piecewise linear trend. These transformations shift the multivariate time-series problem into a feature space with \(p = 70\), where the linear assumption is appropriate.

The daily number of rides (scaled) for 4 Taxi vendors in Chicago.

We predict the future number of rides for 4 providers, using the simulated historical forecasts (SHF) approach of [5], for producing \(K=32\) forecasts at various cutoff points in the history. For cutoff \(k = 0, ..., K −1\), we use the first \(n_{train,k} = n_{start} +k \cdot 7\) days for training, and the next \(n_{test} = 7\) observations for the test set. We then evaluate the performance of the model by the mean squared error (MSE), averaged over all tasks,

SHF example for a single task.

For this data, we get a 2.2% decrease in MSE (in favor of the MTL approach). Although the boost in performance is not mind-blowing, it’s not bad considering we have only tweaked the penalty term in the objective function, to encourage shared sparsity structure between tasks.

The sparsity structure for the STL lasso (top) and the MTL group lasso (bottom), at a single cutoff, with zero entries colored in yellow.

We’ve mentioned that the group lasso penalty produces the same sparsity structure across all tasks. The above plot shows the transposed coefficient matrices (rows for tasks and columns for variables), \(B^T\), for the STL lasso (top) and the MTL group lasso (bottom), with zero entries colored in yellow. We can see that the sparsity structure is indeed shared among tasks in the MTL model, whereas each STL model has its own sparsity structure.

Conclusion

In this post we have introduced the concept of multitask learning and demonstrated it’s power through a simple example of multidimensional time-series forecasting, using group lasso. This model, essentially assumes that the error terms for the different tasks are independent, and that the within-group similarities arise solely through a joint sparsity structure. There are other models that allow one to capture more complex relationships and relatedness among tasks (see e.g. [7], [8]), but we will leave this for future posts.

The code for producing all results and visualizations is available at my GitHub repo.

References and Further Readings

[1] Zhang, Yu, and Qiang Yang. “A survey on multi-task learning.” arXiv preprint arXiv:1707.08114 (2017).
[2] Ruder, S., 2017. An overview of multi-task learning in deep neural networks. arXiv preprint arXiv:1706.05098.
[3] Yuan, Ming and Yi Lin (2006). “Model selection and estimation in regression with grouped variables.” In: Journal of the Royal Statistical Society: Series B (Statistical Methodology) 68.1, pp. 49–67.
[4] Obozinski, Guillaume R, Martin J Wainwright, and Michael I Jordan (2009). “High-dimensional support union recovery in multivariate regression.” In: Advances in Neural Information Processing Systems, pp. 1217–1224.
[5] Sean J. Taylor, Benjamin Letham (2018) Forecasting at scale. The American Statistician 72(1):37-45
[6] Andrew, Harvey C and Shephard Neil (1993). “Structural time series models.” In: Econometrics. Vol. 11. Handbook of Statistics. Elsevier, pp. 261–302.
[7] Rothman, A.J., Levina, E. and Zhu, J., 2010. Sparse multivariate regression with covariance estimation. Journal of Computational and Graphical Statistics, 19(4), pp.947-962.
[8] Navon, A. and Rosset, S., 2018. Capturing Between-Tasks Covariance and Similarities Using Multivariate Linear Mixed Models. arXiv preprint arXiv:1812.03662.