Learning the Pareto Front with Hypernetworks

Multi objective optimization problems are prevalent in machine learning. These problems have a set of optimal solutions, called the Pareto front, where each point on the front represents a different trade-off between possibly conflicting objectives. Recent optimization algorithms can target a specific desired ray in loss space, but still face two grave limitations: (i) A separate model has to be trained for each point on the front; and (ii) The exact trade-off must be known prior to the optimization process. Here, we tackle the problem of learning the entire Pareto front, with the capability of selecting a desired operating point on the front after training. We call this new setup Pareto-Front Learning (PFL).

We describe an approach to PFL implemented using HyperNetworks, which we term Pareto HyperNetworks (PHNs). PHN learns the entire Pareto front simultaneously using a single hypernetwork, which receives as input a desired preference vector, and returns a Pareto-optimal model whose loss vector is in the desired ray. The unified model is runtime efficient compared to training multiple models, and generalizes to new operating points not used during training. We evaluate our method on a wide set of problems, from multi-task learning, through fairness, to image segmentation with auxiliaries. PHNs learns the entire Pareto front in roughly the same time as learning a single point on the front, and also reaches a better solution set. PFL opens the door to new applications where models are selected based on preferences that are only available at run time.

Multi-objective Optimization

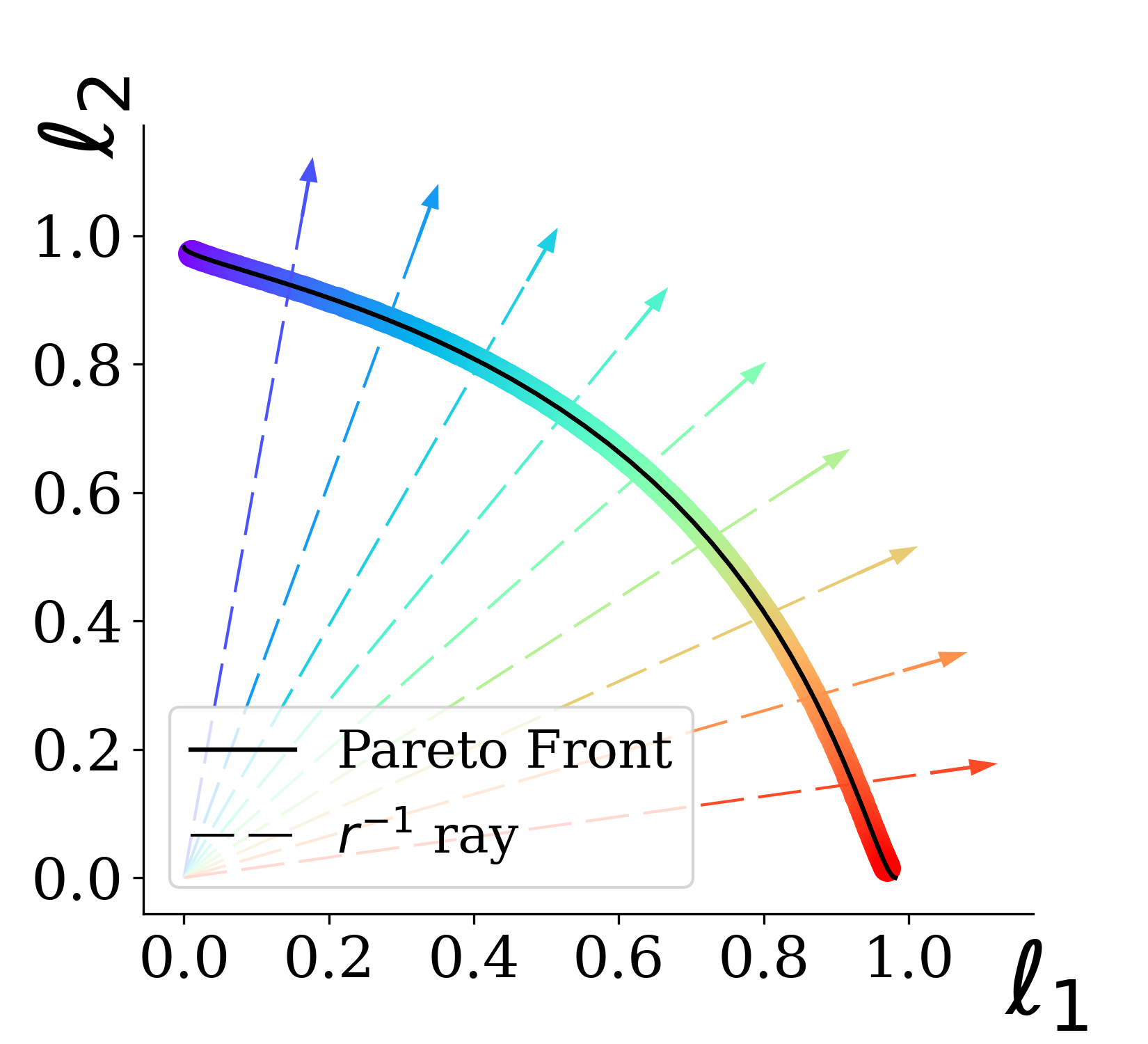
The goal of Multi-Objective Optimization (MOO) is to find Pareto optimal solutions corresponding to different trade-offs between objectives.
Pareto dominance: Solution A (i.e. model) is said to dominate solution B if it is not worst on all objective, and improves B on at least one objective.
Pareto optimality:A point that is not dominated by any other point is called Pareto optimal.
Pareto front:The set of all Pareto optimal points is called the Pareto front.

Pareto Hypernetworks

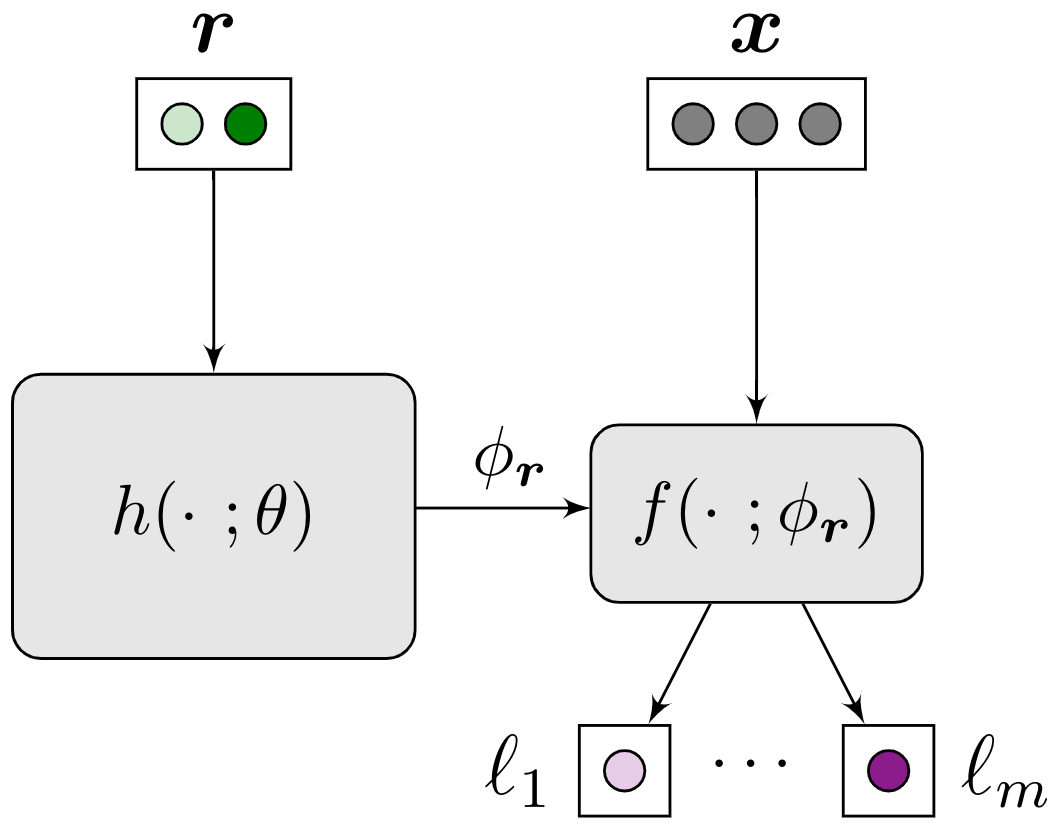
In this work, we propose using a single hypernetwok, termed Pareto HyperNetwork (PHN), to learn the entire Pareto front. PHN acts on a preference vector, that represent a desired trade-off between tasks, to produce the weights of a target network. PHN is optimized to output weights that are (i) Pareto optimal, and; (ii) corresponds to the preference vector.

Experiments

An illustrative example

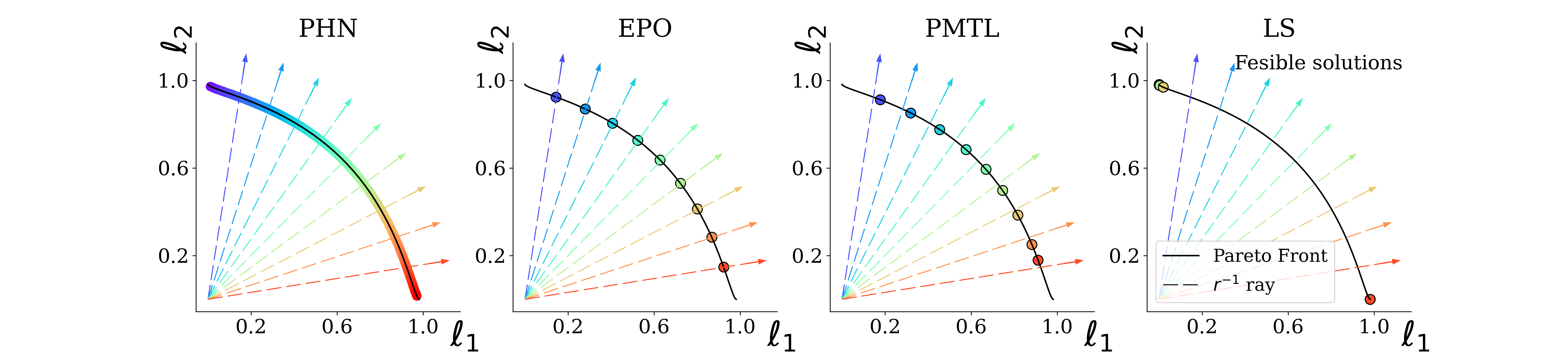
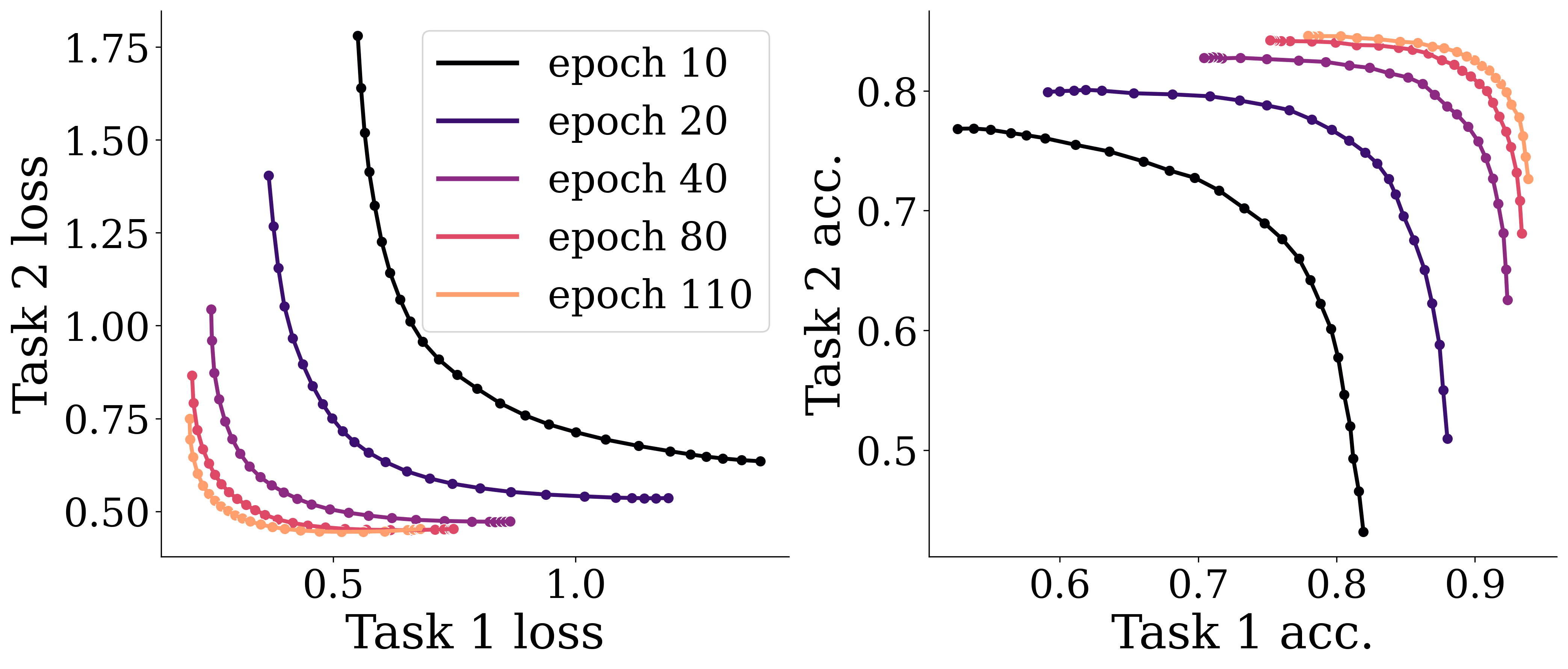
Pareto front (solid line) for 2D loss space and several rays (colored dashed lines) representing various possible preferences. Unlike other approaches that train a model per-ray, a single PHN model converges to the entire Pareto front, mapping any given preference ray to its corresponding solution on the front.

Multi-task classification

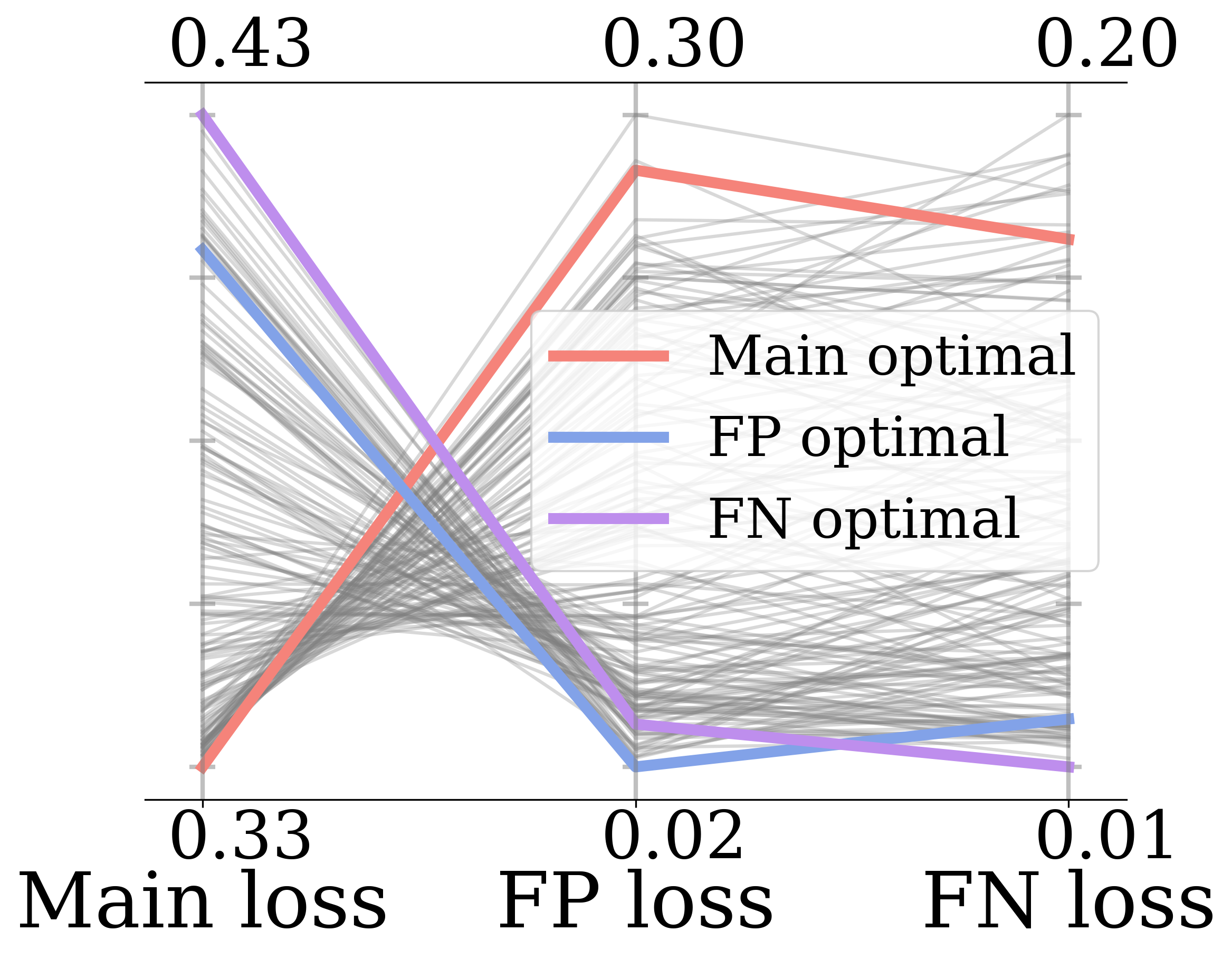
We evaluated PHN using the three Multi-MNIST datasets, a commonly used MOO benchmarks. PHN achives better performance with significantly less training time, compared with baseline methods. The above figure presents the learned Pareto front and corresponding accuracies thought the training process, over the Multi-Fashion + MNIST test set.

Fairness

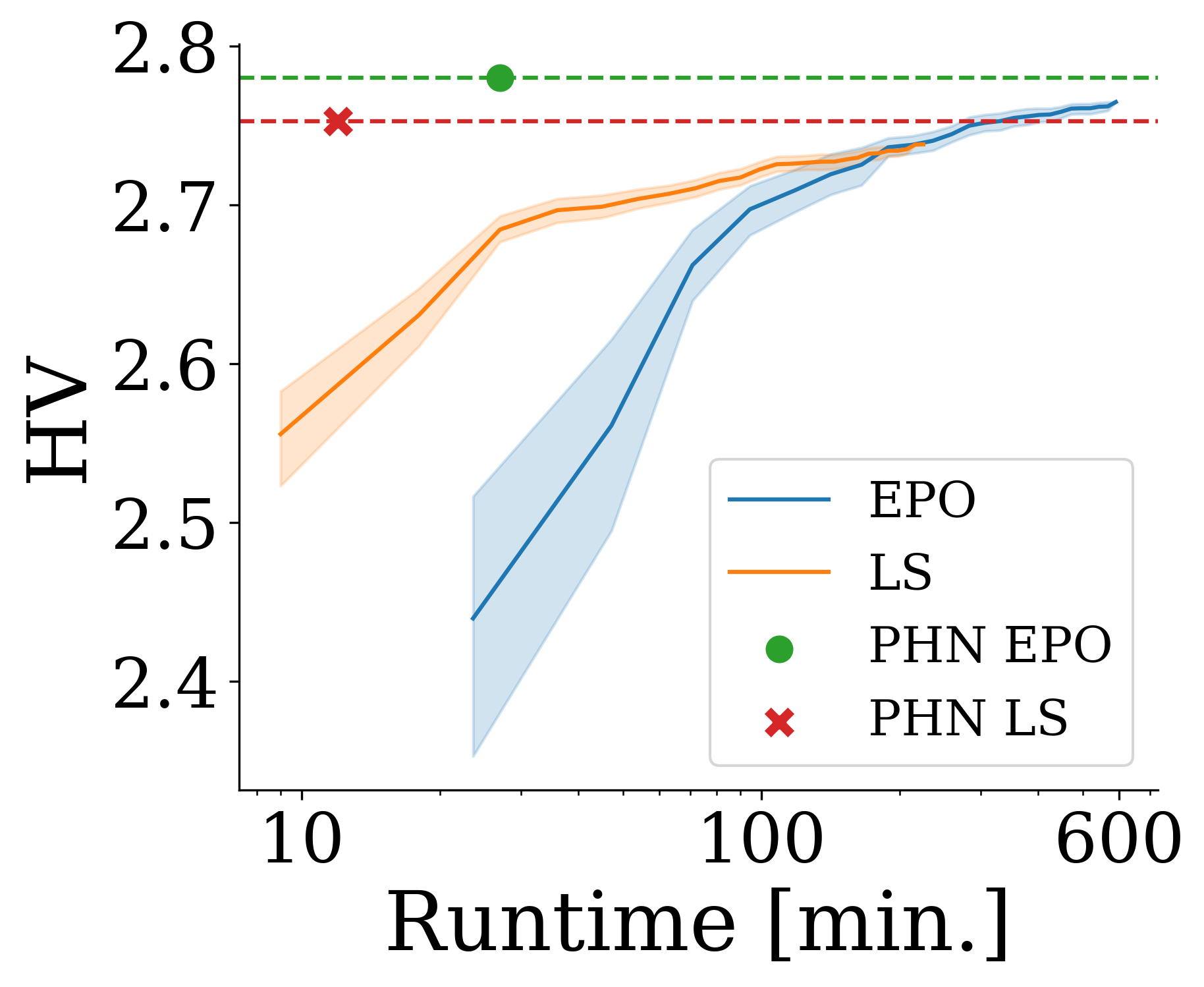
Fairness has become a popular topic in machine learning in recent years, and numerous approaches have been proposed for modeling and incorporating fairness into ML systems. Here, we tackle a 3-dimensional optimization problem, with classification objective, and two fairness objectives: False Positive (FP) fairness, and False Negative (FN) fairness. As before, PHN outperform all baselines, in terms of objective space coverage (measured by Hypervolume), with reduuced training time.

The Quality-Runtime tradeoff

Hypervolume vs. runtime (min.) comparing PHN with preference-specific LS and EPO, on the Multi-Fashion + MNIST dataset. PHN achieves higher HV in significantly less run-time (x-axis in log scale).

PHN learns the entire front in a single model, but the competing methods need to train multiple models to cover the pareto front. As a result, these methods have clear trade off between performance and runtime. We find that PHN can achieve superior overall solutions while being \(10 \sim 50\) times faster.